数字电路技术题目解答第一部分共10题

  【题目1】：模拟信号和数字信号有何区别？各有什么特点？  

【相关知识】：模拟信号、数字信号，及其处理方法。

【解题方法】：理解题。

【解答过程】：通常讲的模拟信号是指该信号的大小随时间连读变化的电信号，不会有突变。如正弦交流电信号，可以用下式表示。它的特点是连读，并能用相位、幅值和时间来描述，有瞬时值，幅值等参数。

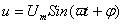
        而数字信号在时间上是离散的，幅值上只区别两个截然不同的值或状态，而并不要求对具体的大小进行量化。两个不同的值或状态可以用二进制数“1”和“0”来表示。两个不同的数值或状态在电路上实现起来非常方便，如开关的闭合或断开，晶体管的饱和导通或截止等等。

  【题目2】：代数法化简和卡诺图法化简有何联系？  

【相关知识】：逻辑函数化简的两种基本方法，1～5变量卡诺图的画法等。

【解题方法】：卡诺图化简其实质是合并最小项，只不过将最小项按一定规律进行排序，并在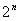个最小项中，提取公共变量后消去其它变量，以达到简化的目的。

【解答过程】：代数法化简逻辑函数式，是运用逻辑代数的定律、定理、规则对逻辑式进行变换，以消除多余的与项和变量。代数法化简没有普遍适用规律，有时需要一定的经验和熟练的技巧。

        卡诺图法化简的实质是合并最小项，以消除多余的变量。因为卡诺图中的一个小方格就是一个最小项，但是小方格与小方格之间的关系必须是相邻的关系，即卡诺图中的上下、左右，前后小方格的最小项必须保持只有一个变量不同，其余的变量都相同，才能实现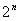（n=1，2，3，…，整正数）个相邻方格的最小项合并。其合并结果是消除n个变量。可见合并的最小项范围越大，可以消除的变量就越多。这样做非常直观、便捷。

        如果在已知与或表达式的情况下，将该式转换成最小项之和式后，再象卡诺图那样找出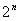个相邻最小项进行合并，就很困难了。可见代数法化简和卡诺图法化简具有相同的内在关系，只是处理方法不一样而已。

  【题目3】：为什么两个二进制数之间的减法运算可以用它们的补码相加来实现？  

【相关知识】：二进制数，二进制数的加法运算，正负二进制数的表示，二进制数的原码、反码和补码表示等。

【解题方法】：可以从日常生活中的时钟校时方法加以理解。联系时钟校时的两种方法，顺时针校时和反时针校时，就可以想到减法可以用补码相加代替了。

【解答过程】：我们已经知道，在数字电路中是用逻辑电路输出的高、低电平表示二进制数的１和０的。那么数的正、负又如何表示呢？通常采用的方法是在二进制数的前面增加一位符号位。符号位为０表示这个数是正数，符号位为１表示这个数是负数。这种形式的数称为原码。

        在作减法运算时，如果两个数是用原码表示的，则首先需要比较两数绝对值的大小，然后以绝对值大的一个作为被减数、绝对值小的一个作为减数，求出差值，并以绝对值大的一个数的符号作为差值的符号。不难看出，这个操作过程比较麻烦，而且需要使用数值比较电路和减法运算电路。如果能用两数的补码相加代替上述的减法运算，那么计算过程中就无需使用数值比较电路和减法运算电路了，从而使运算器的电路结构大为简化。

        为了说明补码运算的原理，我们先来讨论一个生活中常见的事例。例如你在５点钟的时候发现自己的手表停在１０点上了，因而必须把表针拨回到５点。由图E4b20334001-01Z上可以看出，这时有两种拨法：第一种拨法是往后拨５格，（因１０－５＝５），可拨回到５点；另一种拨法是往前拨７格，（因１０＋７＝１７）。由于表盘的最大数是１２，超过１２以后的“进位”将自动消失，于是就只剩下减去１２以后的余数了，即１７－１２＝５，由此也可把表针拨回到５点。这个例子说明，１０－５的减法运算可以用１０＋７的加法运算代替。因为５和７相加正好等于产生进位的模数１２，所以我们称７为－５对模１２的补数，也叫做补码。

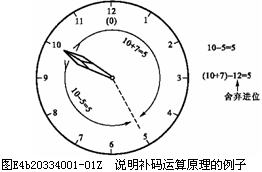
        从这个例子中可以得出一个结论，就是在舍弃进位的条件下，减去某个数可以用加上它的补码来代替。这个结论同样适用于二进制数的运算。

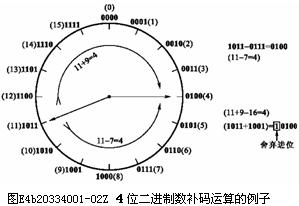
        图E4b20334001-02Z中给出了４位二进制数补码运算的一个例子。由图可见，１０１１－０１１１＝０１００的减法运算，在舍弃进位的条件下，可以用１０１１＋１００１＝０１００的加法运算代替。因为４位二进制数的进位基数是１６（１００００），所以１００１（９）恰好是０１１１（７）对模１６的补码。

        为了避免作减法运算，在求负数的补码时可以先求出二进制数原码的反码（将数字代码中每一位的取值求反，即０改为１，１改为０，符号位保持不变），然后在最低位加１而得到补码。例如有一个４位二进制的负数，它的原码为１０１０１（最左边一位是符号位），则它的反码为１１０１０。在反码的最低位加１后得到补码为１１０１１。将这个补码和它的原码相加(不包括符号位)，得到的正好是１００００（１６），也就是４位二进制数的进位基数，因此１１０１１是１０１０１的补码。

        至此我们可以归纳出以下几点简单的结论：

        １.二进制数原码的定义

        二进制数的原码是在它的数值前面设置一位符号位而得到的。正数的符号位是０，负数的符号位是１。

        ２. 二进制数补码的定义

        正数的补码与原码相同。

        负数的补码可以通过将每一位数值求反，然后在最低位加１而得到（符号位保持不变）。

        ３.两个二进制数的加、减运算都可以用它们的补码相加来实现，得到的运算结果也是补码形式。

        ４. 进一步的分析表明，在将两个数的补码相加时，如果将两个补码的符号位和数值部分产生的进位相加，则得到的和就是两个二进制数相加后代数和的符号。

        例如要计算０１０１－１００１，则可以先求出０１０１和－１００１的补码００１０１和１０１１１（最高位为符号位），再将两个补码相加而得到：

        如果需要求出负数补码对应的原码，只要对这个补码再求一次补码就可以得到了。