数字电路技术题目解答第一部分共10题

  【题目4】：什么是约束项、任意项和无关项？为什么在具有约束条件的逻辑函数化简时，应该尽量使用约束条件。用代数法化简一个逻辑函数时，如何利用约束项使函数化成最简？  

【相关知识】：逻辑运算，逻辑函数，最小项和最大项的概念，逻辑运算中的常用公式，运算规则。

【解题方法】：通过实例，说明什么是约束项、任意茂和无关项，以及它们的异同点。

【解答过程】：我们在分析一个逻辑函数时经常会遇到这样一类情况，就是输入逻辑变量的某些取值始终不会出现。因此，在这些取值下等于１的那些最小项，也将始终为０。这些取值始终为０的最小项，就叫做该函数的约束项。

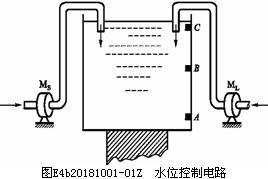
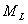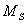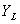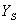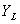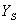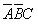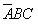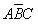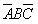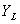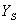        例如要求设计一个逻辑电路，用水箱中水位高度的检测信号Ａ、Ｂ、Ｃ控制两个水泵和的启、停工作状态见图E4b20181001-01Z。如果用和分别表示两个水泵的工作状态，则和为Ａ、Ｂ、Ｃ三个变量的逻辑函数。假定水位高于Ａ、Ｂ、Ｃ中的任何一个检测点时给出的检测信号为１，水位低于任何一个检测点时给出的检测信号为０，则水箱工作过程中ＡＢＣ的取值只可能出现１００、１１０、１１１和０００这四种状态，而不可能出现００１、０１１、１０１和０１０这四种状态，因为水位永远不会高于Ｂ或Ｃ而同时又低于Ａ。因此，与ABC的取值００１、０１１、１０１和０１０对应的四个最小项、、和将永远是０，这四个最小项就是和的约束项。

        既然在工作过程中约束项的值永远是０，那么我们就可以在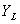和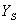的逻辑函数式中加上这些约束项，或不加上这些约束项，而不会影响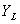和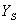的取值。也就是说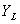和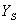的取值与是否加上了约束项没有关系，因此约束项又是逻辑函数式中的无关项。

        在分析和设计逻辑电路时，还可能遇到另外一种情况，就是在输入变量的某些取值下，逻辑函数值等于１还是等于０都可以，对电路的逻辑功能没有影响。在这些变量取值下等于１的那些最小项，就叫做这个逻辑函数的任意项。

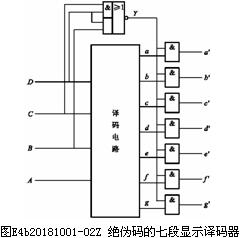
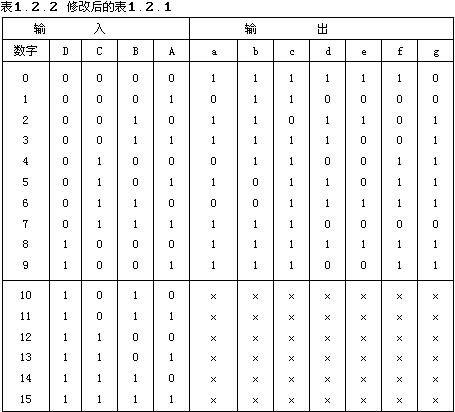
        例如要设计一个拒绝伪码的七段显示译码器，其真值表如表１.２.１。所谓拒绝伪码，系指在输入为１０１０～１１１１时输出无任何字形显示，即ａ～ｇ输出全都等于０。

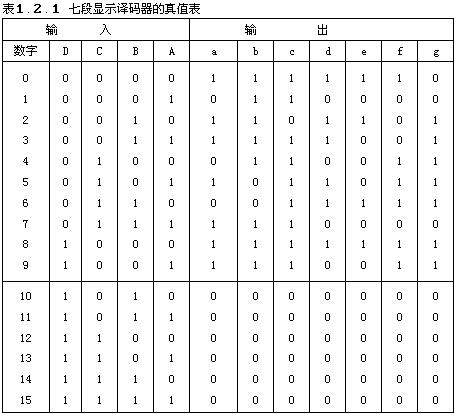
        由表１.２.１可以看出，这个译码器是一个有４个输入变量和７个输出函数的组合逻辑电路。如果我们采用图E4b20181001-01Z的电路结构，在ａ～ｇ的输出端增加一级缓冲器，同时还在缓冲器的输入增加一个控制信号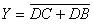，那么当ＤＣＢＡ＝１０１０～１１１１时，不论ａ～ｇ是１还是０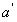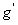，～肯定等于０，所以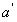～仍然符合表１.２.１的要求。

        这就是说，当ＤＣＢＡ取值为１０１０～１１１１时，ａ～ｇ每个函数输出的取值是１或０都可以，不影响最后的输出～。因此，在ＤＣＢＡ取值为１０１０～１１１１时，其值为１的六个最小项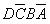、、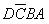、、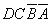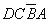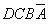和为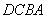数ａ～ｇ的任意项。在化简ａ～ｇ的逻辑函数式时，既可以在式中写入这些任意项，也可以不写进这些任意项，所以任意项也是逻辑函数式中的无关项。这样我们就可以把表１.２.１改写为表１.２.２的形式了。表中的×仍然表示无关项。

        虽然任意项和约束项都是逻辑函数式中的无关项，但二者是有区别的。因为约束项的取值永远是０，所以在逻辑函数式中无论写入约束项还是去掉约束项，都不会改变函数的输出值。而任意项则不同，当我们在逻辑函数式中写入某个任意项之后，则输入变量的取值使这个任意项的值为１时，函数的输出值也为１；如果从逻辑函数式中将这个任意项拿掉，则输入变量取值使这个任意项的值为１时，函数的输出值等于０。

  【题目5】：如何判断一个逻辑函数已化到了最简？化简逻辑函数有什么实际意义？  

【相关知识】：逻辑函数的与或表达式和逻辑函数的代数法化简等。

【解题方法】：为了便于实现逻辑电路，逻辑函数常用“与或”表达式表示。因此，是否化到最简主要看与项数目和每个与项所包含的变量数是否最少。

【解答过程】：一个与或表达式是否已达到最简，主要看两个方面：一是表达式中“与”项的数目是否最少了，即表达式中的与项是否不能再合并了；第二是在与项相同的条件下，检查每个与项所包含的变量数是否达到了最少。因为减少与项可以节省与门个数，减少与项中的变量数可以减少门的输入端个数。

  【题目6】：逻辑函数的不同表示方法之间是如何进行转换的？  

【相关知识】：逻辑函数真值表、逻辑函数的与或表达式、卡诺图、最小项、标准与或表达式。

【解题方法】：通过1.由真值表求逻辑函数式；2.由逻辑函数式求真值表；3.卡诺图与逻辑函数表达式之间的转换，一、一加以说明。

【解答过程】：同一个逻辑问题，可以采用多种方法表示。而这些描述同一个问题的逻辑表示之间都能实现方便的转换。

        1.由真值表求逻辑函数式和逻辑电路

        把真值表中使逻辑函数值为1的输入变量组合写成对应的与项。若对应的变量取值为1，则写成原变量；若对应的变量取值为0，则写成反变量。然后将这些与项全部“或”起来，就得到了逻辑函数式。

        对应于逻辑函数式的反变量，采用非门逻辑符号；与项用与门逻辑符号，多个与项相“或”用或门逻辑符号；将它们按逻辑运算关系连接起来，就能得到实现逻辑要求的逻辑电路。

        2. 由逻辑函数式求真值表

        只要把逻辑函数式中所有输入变量按“0”、“1”取值，代入所有组合中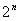（—n是函数的变量数）进行运算，求出相应的逻辑函数值（结果）填入真值表中的相应行即可。

        3. 卡诺图与逻辑函数表达式之间的转换

        先将逻辑函数化为最小项之和的形式（即标准与或表达式），接着画出与函数变量数相对应的卡诺图，在卡诺图中，凡是与表达式对应的最小项的小方格内填入“1”，其他小方格内填入“0”。这样便得到了逻辑函数式的卡诺图。