数字电路技术题目解答第四部分共11题

  【题目5】：应用中规模集成计数器设计一般时序电路的方法？  

【相关知识】：中规模集成计数器的应用，状态变量的确定，状态真值表，状态转移图，时序电路设计的一般方法等。

【解题方法】：需要具备记忆功能的数字电路必须是时序电路。时序电路也称为状态机（state machine）电路。设计时序电路必须确定电路的外部输入和外部输出，其中最关键的是确定电路可能存在的各种状态。

        如果状态转移图中状态连续变化，或者转换过程不受外部输入的控制，应用中规模集成计数器为核心设计时序电路完整设计流程是：

        （1） 确定时序电路的状态数和状态转移图，确定电路的外部输出；

        （2） 设总状态数是M，应用中规模集成计数器设计一个状态连续变化的M进制计数器；

        （3） 对计数器的状态变量进行译码得到外部输出，设计框图如图1所示。

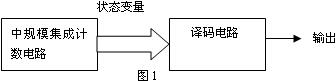
        如果时序电路有外部输入变量，状态之间的转换关系比较复杂、受外部输入控制，应用中规模集成计数器为核心的设计时序电路的流程是：

        （1） 确定电路的外部输入和外部输出；

        （2） 确定电路的所有原始状态，并确定各状态随着外部输入（包括时钟输入）变化时状态之间的转换关系，得到原始状态转移图；

        （3） 简化原始状态转移图；

        （4） 确定状态分配方法，决定中规模集成计数器的个数；

        （5） 利用置数和计数交替法确定中规模集成计数器的置数控制端和置数输入端，列出状态真值表

        （6） 通过卡诺图法简化，得到集成计数器的置数控制端方程和置数输入端方程；画出完整的逻辑电路图。

【解答过程】：

        [例1] 已知中规模集成计数器74LS161的电路框图如，功能表如表1所示。试用74LS161设计一个1100110001序列脉冲发生器。

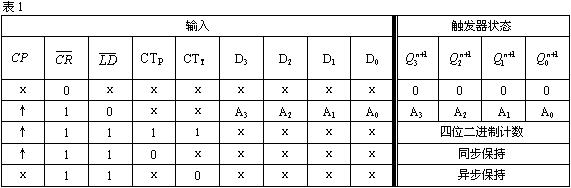
        [解] 1100110001序列共有十个状态，利用中规模集成计数器设计一个十进制计数器，然后对计数器的状态变量译码，产生1100110001序列。设十进制计数器的状态转换图如图2。

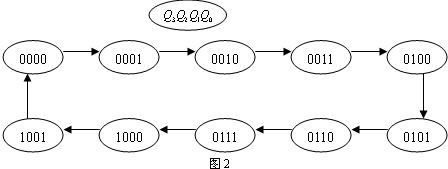
        利用反馈清零法设计该状态转换图，十进制计数器电路如图3。

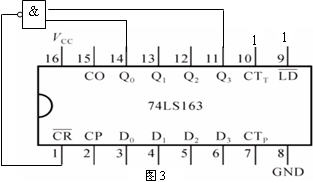
        设计输出序列信号为Z，Z由中规模集成计数器的状态变量译码得到，十个状态与序列信号“1100110001”相对应，故译码部分的卡诺图如图4。

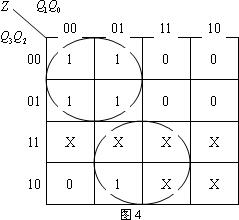
        简化得：

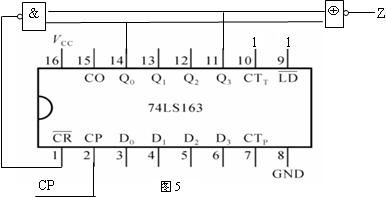
        1100110001序列脉冲发生器的完整逻辑电路图如图5所示：

        例2，应用中规模集成计数器74LS161设计110序列检测电路。

        [解]序列信号检测电路通过时钟有效边沿检测输入信号的电平状态。

        （1）确定电路的外部输入和外部输出；

        对于110序列检测电路，连续三个时钟边沿检测到输入信号的状态分别是1、1、0时，输出一个电平信号。设110序列脉冲检测电路的外部输入是X，输出信号是Z，时钟信号是CP，时钟有效状态是下降沿。

        （2）确定电路的原始状态和原始状态转换图

        110序列检测电路可能存在的状态是：

        初始状态S0：时钟有效沿时，输入信号是低电平；

        状态S1：时钟有效沿检测到输入信号是高电平；

        状态S2：连续两个时钟有效沿检测到输入信号是高电平；

        状态S3：前两个时钟有效沿检测到输入信号是高电平，第三个时钟有效沿检测到低电平，此时检测到110序列。

        根据状态定义可得到原始状态图如图6(a)所示。

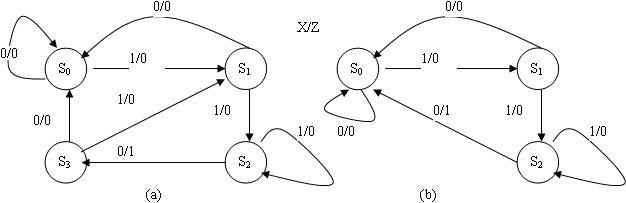
图6

        （3）简化原始状态转移图；

        图1原始状态状态转换图中，

        显然S3状态与S0状态等效，状态S3可以简化掉，原始状态图可简化成图6（b）。

        （4）得到数字化状态转移图

        三个状态至少需要二只触发器。二只触发器共有四个状态，分别是00，01，10和11。将四个状态分配给S0、S1、S2，共有种组合。针对不同的状态分配，设计结果的简单与复杂程序会略有区别，其中存在一个最优算法。本例，仅简单按自然顺序给予分配，设S0=00，S1=01，S2=10，两只触发器的状态分别是(q1)，(q0)，数字化后的状态转换图如图7所示。

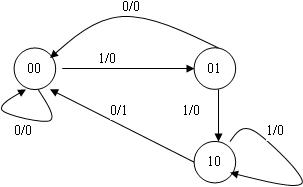
图7

        110序列检测电路只有3个状态变量，只需要二只触发器，一只集成计数器74LS161已足够。

        （5）将状态转移图转换成状态真值表

        首先按规范形式列出真值表的输入部分（本例只需用到74LS161内部的二只触器的状态输出(q1)，(q0)），然后根据状态转换图，逐行填入次态值和外部输出值，并决定是计数还是置数，若是置数，还需要确定置数输入值。完整状态真值表如表2所示。

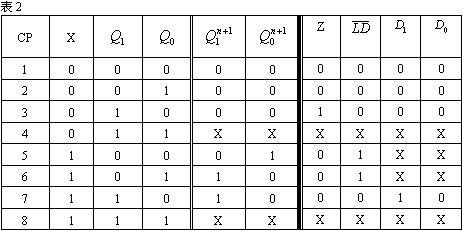
        其中，状态11并没有在状态转换图中出现，属于无关项输入，输出可填任意状态“X”，设计完毕后必须检测自启动。

        （6）计算集成计数器的置数控制端方程和置数输入端方程；

        用卡诺图法法简化后可得：，，，

        当时，，次态；当时，，次态，电路能够自启动。

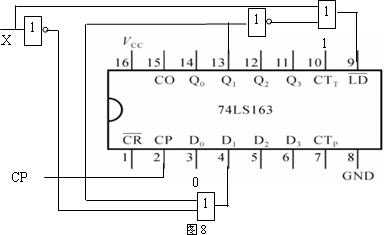
        （7） 完整的逻辑电路图如图8所示。